Introdução
A marcação a mercado ajusta diariamente o preço de um título ao valor que seria negociado hoje. Quando a taxa de juros sobe, o preço do título cai; quando a taxa cai, o preço sobe. Para estimar quanto o preço pode variar, usamos três medidas: duration, convexidade e a sensibilidade (combinação das duas).
Exemplo base (que usaremos nas contas)
- Valor de face (FV): R$ 1.000
- Cupom: 10% a.a. (R$ 100 ao ano)
- Prazo: 5 anos
- Taxa de mercado (YTM): 12% a.a.
Os fluxos: \( CF_1=CF_2=CF_3=CF_4=100 \) e \( CF_5=1{.}100 \).
1) Como chegamos à Duration (com números)
(a) Desconto de cada fluxo
\[
PV_t=\frac{CF_t}{(1+y)^t}
\]
Com \(y=12\%\):
\[
\begin{aligned}
PV_1 &= \frac{100}{(1{,}12)^1} = 89{,}29 \\
PV_2 &= \frac{100}{(1{,}12)^2} = 79{,}72 \\
PV_3 &= \frac{100}{(1{,}12)^3} = 71{,}18 \\
PV_4 &= \frac{100}{(1{,}12)^4} = 63{,}55 \\
PV_5 &= \frac{1{.}100}{(1{,}12)^5} = 624{,}17
\end{aligned}
\]
(b) Preço = soma dos PVs
\[
P = 89{,}29+79{,}72+71{,}18+63{,}55+624{,}17 = 927{,}90
\]
(c) Pesos (importância de cada fluxo)
\[
w_t = \frac{PV_t}{P}
\]
\[
\begin{aligned}
w_1 &= 0{,}0962 \\
w_2 &= 0{,}0859 \\
w_3 &= 0{,}0767 \\
w_4 &= 0{,}0685 \\
w_5 &= 0{,}6727
\end{aligned}
\]
(d) Duration de Macaulay
\[
D_{mac} = \sum t \cdot w_t = 4{,}14 \; \text{anos}
\]
(e) Duration Modificada
\[
D_{mod} = \frac{4{,}14}{1{,}12} = 3{,}69
\]
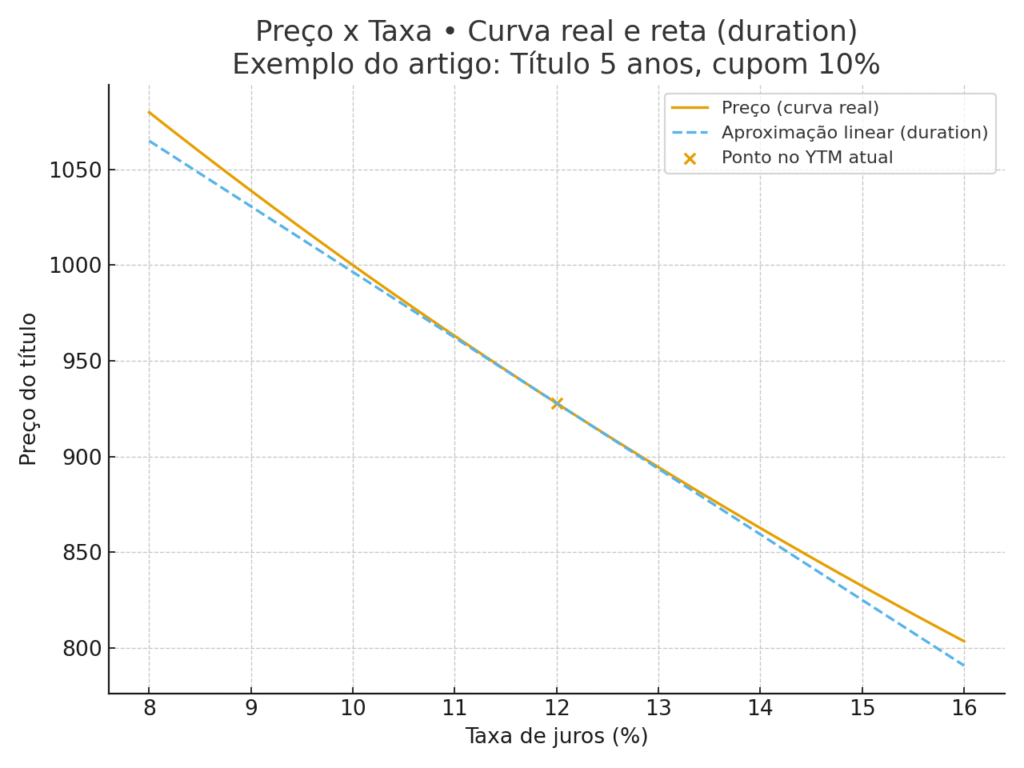
Leitura: uma alta de 1 p.p. nos juros gera queda de ~3,69% no preço.
2) Como chegamos à Convexidade (com números)
\[
Conv = \frac{\sum CF_t \cdot t(t+1) / (1+y)^{t+2}}{P}
\]
\[
\begin{aligned}
t=1 &:\; 142{,}36 \\
t=2 &:\; 381{,}31 \\
t=3 &:\; 680{,}91 \\
t=4 &:\; 1{.}013{,}26 \\
t=5 &:\; 14{.}927{,}52
\end{aligned}
\]
Soma = 17.145,36 →
\[
Conv = \frac{17.145,36}{927,90} = 18,48
\]
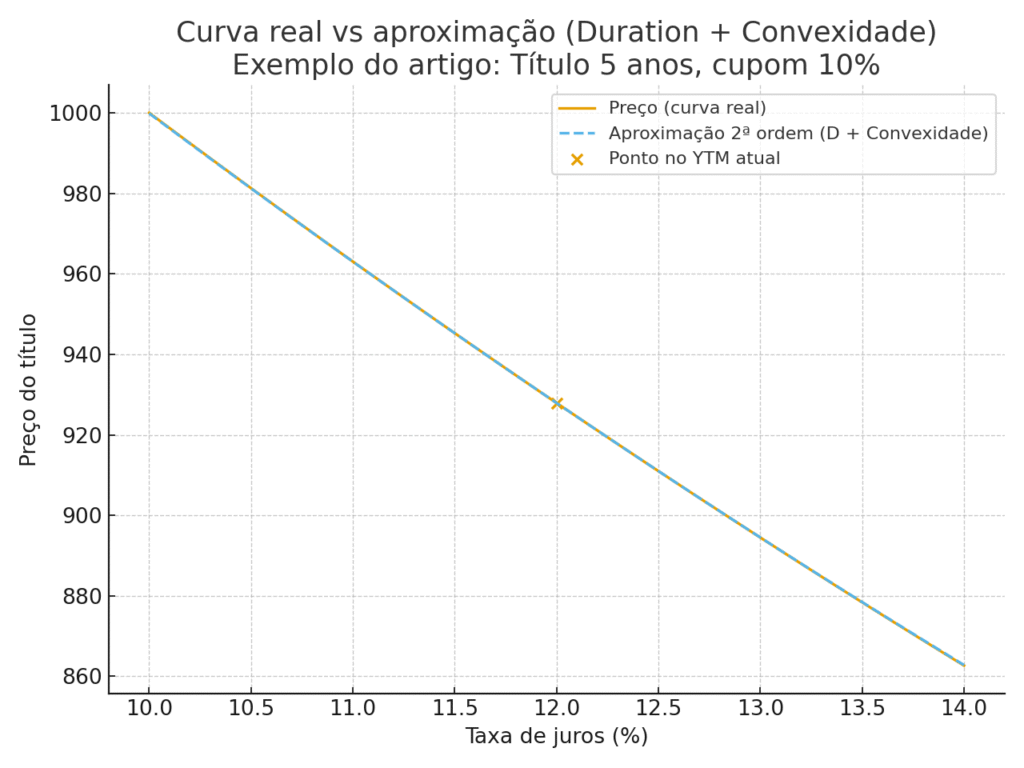
3) Sensibilidade: Duration + Convexidade (com valores em R$)
\[
\frac{\Delta P}{P} \approx -D_{mod}\cdot \Delta i + \tfrac{1}{2}\cdot Conv \cdot (\Delta i)^2
\]
Com \( D_{mod}=3,6924 \), \( Conv=18,4775 \), e preço \( P=927,90 \):
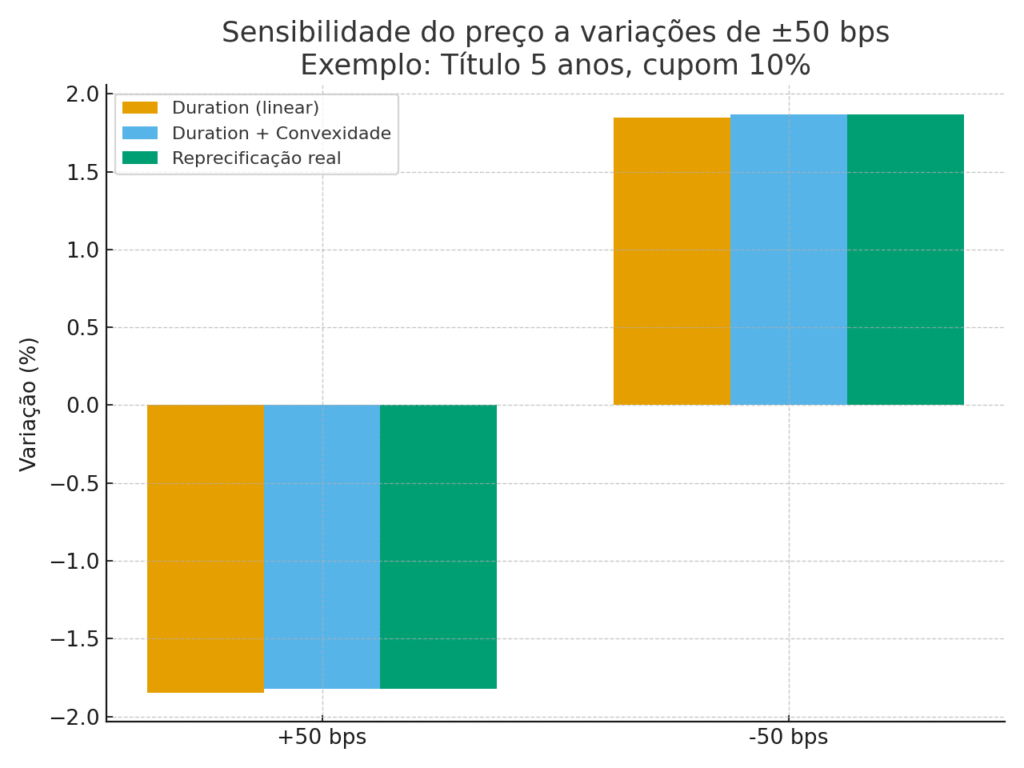
🟠 Caso 1 — Alta de +0,50 p.p. \((\Delta i = +0{,}005)\)
\[
\begin{aligned}
\Delta P/P &= -D_{mod}\cdot \Delta i + \tfrac{1}{2}\cdot Conv \cdot (\Delta i)^2 \\[6pt]
&= -3{,}6924 \cdot 0{,}005 + 0{,}5 \cdot 18{,}4775 \cdot (0{,}005)^2 \\[6pt]
&= -0{,}018462 + 0{,}000231 \\[6pt]
&= -0{,}018231 \quad \Rightarrow \quad -1{,}8231\%
\end{aligned}
\]
\[
\Delta P = -1{,}8231\% \times 927{,}90 \approx -16,92
\]
\[
P_{novo} = 927{,}90 – 16,92 \approx \mathbf{R\$\,910,98}
\]
🟢 Caso 2 — Queda de −0,50 p.p. \((\Delta i = -0{,}005)\)
\[
\begin{aligned}
\Delta P/P &= -3{,}6924 \cdot (-0{,}005) + 0{,}5 \cdot 18{,}4775 \cdot (0{,}005)^2 \\[6pt]
&= +0{,}018462 + 0{,}000231 \\[6pt]
&= +0{,}018693 \quad \Rightarrow \quad +1{,}8693\%
\end{aligned}
\]
\[
\Delta P = +1{,}8693\% \times 927{,}90 \approx +17,34
\]
\[
P_{novo} = 927{,}90 + 17,34 \approx \mathbf{R\$\,945,24}
\]
Como usar na prática
- Comparar títulos: maior duration = maior sensibilidade.
- Planejar liquidez: cuidado com durations longas se precisar do dinheiro antes do vencimento.
- Ciclo de juros: em queda de juros, títulos longos se valorizam mais.
Insight
“Pense na duration como o termômetro (intensidade e direção) e na convexidade como o ajuste fino que aproxima a conta da realidade.”
Conclusão
A renda fixa não é fixa no meio do caminho. O preço varia com os juros. Com duration e convexidade você consegue prever essa variação, evitar sustos e até aproveitar oportunidades. Se levar até o vencimento, recebe a taxa contratada, se vender antes, o preço dependerá da marcação a mercado.